The Theory of Classification

Object-oriented programming languages were originally developed in advance of any formal theory of classification and, as a result, their treatment of class was muddled and ill-founded. Strongly-typed languages assumed that the notion of class was equated with type, and behavioural compatibility could be described using a terminology of types and subtyping, which strictly did not apply. The type systems of languages affected by such misunderstandings were sometimes incorrect. Other languages assumed that objects have class and type independently, relegating the notion of class to a mere implementation construct.

To counter this confusion, a mathematical theory of classification was developed, which encompassed other approaches to type abstraction, such as "type constructors", "generic parameters", "classes", "inheritance" and "polymorphism". The theory extended earlier work on F-bounded polymorphism by providing second- and higher-order typed record combination for objects modelled as records of functions. The theory captures notions such as single, multiple and mixin inheritance and unifies the treatment of generic polymorphism with inheritance-based polymorphism. Object-oriented languages such as Smalltalk, C++, Eiffel and Java may be explained within the theory, which also shows how the syntactic treatment of type polymorphism may be simplified in future object-oriented languages.

Project History

This project grew out of a personal dissatisfaction with the various ad-hoc typing mechanisms used to express polymorphism in object-oriented programming languages. Inspired by Cook's account of how a strongly-typed object-oriented language violated mathematical subtyping, by permitting covariant specialisation of method argument types [1], work started on an object-oriented language, which was to support strict subtyping (Simons, 1991) and whose subtyping rules also regulated the permissible refinements of pre- and postconditions (Simons, 1994a).

Subsequently, the type system of this language, Brunel, was completely redesigned to accommodate Cook's new theory of F-bounded polymorphism, which treated a class as a second-order construct in the function-bounded polymorphic λ-calculus [2], [3]. From this, an initial approach was developed to unify the object-oriented notion of inclusion polymorphism with more traditional notions of parametric polymorphism and type constructors (Simons and Cowling, 1992). The unified theory of classification was summarised in (Simons, 1996a) and was presented as tutorials at ECOOP and OOPSLA (Simons, 1993a, 1993b, 1994b), in which the consequences of adopting an F-bounded type system were explored. A class is a function-bounded second-order construct in the λ-calculus, whereas an object type is the least fixed point, a first-order construct. Different parametric type checking rules apply, which permit the covariant specialisation of method argument types, as object-oriented languages intuitively seem to require.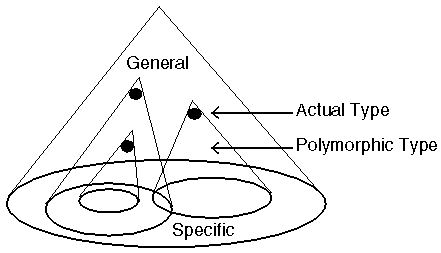

The unified theory of classification was the subject of the PhD thesis (Simons, 1995a), which also described the Brunel 2.0 language as an exemplar of the new type system. This presented a unified treatment of inheritance and genericity (templates), showing how the interactions of different kinds of extension and specialisation by inheritance and by parametric specialisation and substitution are confluent. This eventually extended Cook's model from second-order to higher-order, but could be approximated by dependent second-order types some of the time, such as the treatment of mixins in (Simons, 1995b). The impact of the theory upon another object-oriented language, Eiffel, was described in (Simons, 1995c, 1995d). This provided an alternative second-order, F-bounded solution to the type-failure problem, which Cook had addressed earlier using first-order subtyping [1]. The revised solution permitted covariant method argument specialisation, as found in Eiffel, but also replaced three different syntactic mechanisms for expressing polymorphism (conformance, anchored types, constrained genericity) by a single mechanism. The popular impact of the theory of classification upon language terminology and design notation was discussed in (Simons, 1996b).

Most recently, the Theory of Classification has reached a much wider audience, through the publication of an invited series of articles in the Journal of Object Technology. This is a popular monograph, serialised in 20 parts (Simons, 2002 - 2005). This material has over 100 citations and is collated on a number of specialist websites, such as the community weblog for programming language research, Lambda the Ultimate. The material has formed the basis for a number of courses on object-oriented type theory at the Universities of Berne (Switzerland), Sheffield (UK) and others.

[1] W Cook, A proposal for making Eiffel type-safe, Proc 3rd European Conf. Object-Oriented Progr., 57-70; reprinted in Computer Journal, 32 (4), (Nottingham: BCS/Pitman, 1989), 305-311.

[2] P Canning, W Cook, W Hill, W Olthoff and J Mitchell, F-bounded polymorphism for object-oriented programming, Proc 4th Int. Conf. Func. Progr. Lang. and Arch., September, (London: Imperial College, 1989), 273-280.

[3] W Cook, W Hill and P Canning, Inheritance is not subtyping, Proc 17th ACM Symp. Principles of Progr. Lang., (ACM Press, 1990), 125-135.

Related Publications

The Theory of Classification is published as a popular monograph, serialised in 20 parts from 2002-2005 in the Journal of Object Technology. Links to the published articles are given below. In Spring 2008, the journal changed the location of these articles. The links have been updated.

• A J H Simons, The Theory of Classification, Part 1: Perspectives on Type Compatibility, Journal of Object Technology, 1 (1), May-June, ed. R Wiener, (Zurich: ETH, 2002), 55-61.
  Erratum: there is a missing axiom 3 on page 60. This is corrected in The Theory of Classification, Part 5, page 15.
• A J H Simons, The Theory of Classification, Part 2: The Scratch-Built Typechecker, Journal of Object Technology, 1 (2), July-August, ed. R Wiener, (Zurich: ETH, 2002), 47-54.
• A J H Simons, The Theory of Classification, Part 3: Object Encodings and Recursion, Journal of Object Technology, 1 (4), September-October, ed. R Wiener, (Zurich: ETH, 2002), 49-57.
• A J H Simons, The Theory of Classification, Part 4: Object Types and Subtyping, Journal of Object Technology, 1 (5), November-December, ed. R Wiener, (Zurich: ETH, 2002), 27-35.
• A J H Simons, The Theory of Classification, Part 5: Axioms, Assertions and Subtyping, Journal of Object Technology, 2 (1), January-February, ed. R Wiener, (Zurich: ETH, 2003), 13-21.
• A J H Simons, The Theory of Classification, Part 6: The Subtyping Inquisition, Journal of Object Technology, 2 (2), March-April, ed. R Wiener, (Zurich: ETH, 2003), 17-26.
• A J H Simons, The Theory of Classification, Part 7: A Class is a Family of Types, Journal of Object Technology, 2 (3), May-June, ed. R Wiener, (Zurich: ETH, 2003), 13-22.
• A J H Simons, The Theory of Classification, Part 8: Classification and Inheritance, Journal of Object Technology, 2 (4), July-August, ed. R Wiener, (Zurich: ETH, 2003), 55-64.
• A J H Simons, The Theory of Classification, Part 9: Inheritance and Self-Reference, Journal of Object Technology, 2 (6), November-December, ed. R Wiener, (Zurich: ETH, 2003), 25-34.
• A J H Simons, The Theory of Classification, Part 10: Method Combination and Super-Reference, Journal of Object Technology, 3 (1), January-February, ed. R Wiener, (Zurich: ETH, 2004), 43-53.
• A J H Simons, The Theory of Classification, Part 11: Adding Class Types to Object Implementations, Journal of Object Technology, 3 (3), March-April, ed. R Wiener, (Zurich: ETH, 2004), 7-19.
• A J H Simons, The Theory of Classification, Part 12: Building the Class Hierarchy, Journal of Object Technology, 3 (5), May-June, ed. R Wiener, (Zurich: ETH, 2004), 13-24.
• A J H Simons, The Theory of Classification, Part 13: Template Classes and Genericity, Journal of Object Technology, 3 (7), July-August, ed. R Wiener, (Zurich: ETH, 2004), 15-25.
• A J H Simons, The Theory of Classification, Part 14: Modification and Objects like Myself, Journal of Object Technology, 3 (8), September-October, ed. R Wiener, (Zurich: ETH, 2004), 15-26.
• A J H Simons, The Theory of Classification, Part 15: Mixins and the Superclass Interface, Journal of Object Technology, 3 (10), November-December, ed. R Wiener, (Zurich: ETH, 2004), 7-18.
• A J H Simons, The Theory of Classification, Part 16: Rules of Extension and the Typing of Inheritance, Journal of Object Technology, 4 (1), January-February, ed. R Wiener, (Zurich: ETH, 2005), 13-25.
• A J H Simons, The Theory of Classification, Part 17: Multiple Inheritance and the Resolution of Inheritance Conflicts, Journal of Object Technology, 4 (2), March-April, ed. R Wiener, (Zurich: ETH, 2005), 15-26.
• A J H Simons, The Theory of Classification, Part 18: Polymorphism Through the Looking Glass, Journal of Object Technology, 4 (4), May-June, ed. R Wiener, (Zurich: ETH, 2005), 7-18.
• A J H Simons, The Theory of Classification, Part 19: The Proliferation of Parameters, Journal of Object Technology, 4 (5), July-August, ed. R Wiener, (Zurich: ETH, 2005), 37-48.
• A J H Simons, The Theory of Classification, Part 20: Modular Checking of Classtypes, Journal of Object Technology, 4 (7), September-October, ed. R Wiener, (Zurich: ETH, 2005), 7-18.

Other related publications described in the history above are given below:

• A J H Simons, Brunel: a strongly-typed, portable object-oriented language and programming environment, Department of Computer Science Research Report CS-91-07, (Sheffield: DCS, 1991).
• A J H Simons and A J Cowling, A proposal for harmonising types, inheritance and polymorphism for object- oriented programming, Department of Computer Science Research Report CS-92-13, (Sheffield: DCS, 1992).
• A J H Simons, Introduction to Object-Oriented Type Theory, ECOOP '93 Tutorial 10, (Kaiserslautern : AITO/ACM Press, 1993), 62pp.
• A J H Simons, Introduction to Object-Oriented Type Theory, OOPSLA '93 Tutorial 23, (Washington : ACM Press, 1993), 62pp.
• A J H Simons, Adding axioms to Cardelli-Wegner subtyping, Department of Computer Science Research Report CS-94-6, (Sheffield: DCS, 1994).
• A J H Simons, Exploring Object-Oriented Type Systems, OOPSLA '94 Tutorial 28, (Portland : ACM Press, 1994), 81pp.
• A J H Simons, A Language with Class: The Theory of Classification Exemplified in an Object-Oriented Programming Language, PhD Thesis, Department of Computer Science, University of Sheffield (Sheffield, 1995).
• A J H Simons, Mixins: typing the superclass interface, Department of Computer Science Research Report CS-95-26, (Sheffield: DCS, 1995).
• A J H Simons, A different proposal for making Eiffel type-consistent, Department of Computer Science Research Report CS-95-07, (Sheffield: DCS, 1995). See revised TOOLS paper.
• A J H Simons, Rationalising Eiffel's type system, Proc. 18th Conf. Technology of Object- Oriented Languages and Systems (TOOLS Pacific), eds. C. Mingins, R. Duke and B. Meyer (Melbourne, 1995), 365-377.
• A J H Simons, A theory of class, Proc. 3rd Int. Conf. Object-Oriented Info. Sys., eds. D Patel, Y Sun and S Patel, (London: Springer Verlag, 1996), 44-56.
• A J H Simons, Let's agree on the meaning of class, Department of Computer Science Research Report CS-96-26, (Sheffield: DCS, 1996).