Speech Recognition by Dynamic Time Warping

Asymmetrical DTW Algorithm

Although the basic DP algorithm (Eq. 1) has the benefit of symmetry (i.e. all frames in both input and reference must be used) this has the side effect of penalising horizontal and vertical transitions relative to diagonal ones.

EXERCISE: Convince yourself that this is so by considering the different ways of going from (i-1,j-1) to (i,j).

One way to avoid this effect is to double the contribution of d(i,j) when a diagonal step is taken. This has the effect of charging no penalty for moving horizontally or vertically rather than diagonally. This is also not desirable (why?), so independent penalties d_h and d_v can be applied to horizontal or vertical moves. In this case (1) becomes:

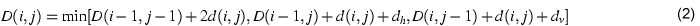
Suitable values for d_h and d_v may be found experimentally.

This approach will favour shorter templates over longer templates, so a further refinement is to normalize the final distance score by template length to redress the balance.

If we restrict the allowable path transitions to be:

• (i-1,j-2) to (i,j) - extended diagonal (skips a template frame - diagonal slope 2)
• (i-1,j-1) to (i,j) - standard diagonal (slope 1)
• (i-1,j) to (i,j) - horizontal (duplicates a template frame - slope 0)

then we are assume that each frame of the input pattern is used once and only once. This means that we can dispense with template-length normalization and it is not required to add the local distance in twice for diagonal (slope 1) path transitions. This approach is referred to as asymmetric dynamic programming.


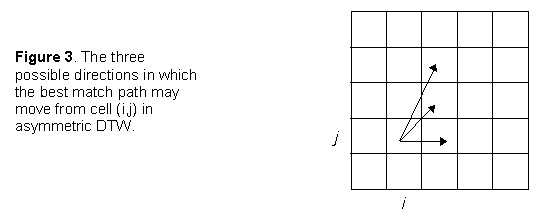
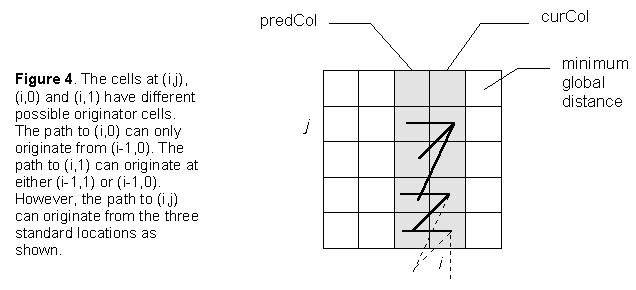
However, it should be noted that special cases do occur. Consider the path as it originates from (0,0). As the path must move to column 1 then the global distances to rows 1, 2,... of the first column are meaningless, as illustrated in Figure 5.

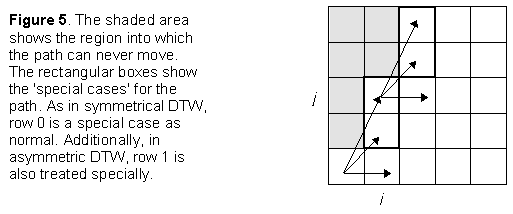
Now consider the point (i,j) in Figure 5. This can be considered a 'special case'. Special cases arise by virtue of the fact that the path must to move along the pattern file one frame at a time. This means that the match path can only arrive in such a 'special case' cell from a limited number of locations. As can be seen from Figure 5, such special cases appear in pairs which are located progressively higher in each subsequent column until a pair (or half of a pair if the column height is even) is located at the top of a column. All the remaining columns can be dealt with as normal. The special cases, when they occur, are at j = 2i-1 and 2i. The global cost for each is:

• 2i-1: local cost + minimum global distance at predCol[j-1] and predCol[j-2]
• 2i: local cost + global distance at predCol[j-2]

For both normal cells and special case cells, the rows 0 and 1 are dealt with in a different manner than normal.

The algorithm to find the least global cost is now more complicated than the symmetrical version. Therefore, it is easier to explain in pseudocode immediately rather than explaining the process in words. The pseudocode for the process is:

Note that the minimum cost is the value in the last column at highestJ. This deals with the problem in Figure 6. As each row is processed, the highest reachable row index is stored in highestJ.

Once again, in order to effect a recogniser, the input pattern is taken and the above process is repeated for each template file. The template file which gives the lowest global cost is the word estimate.