Accurate Multi-dimensional
Poisson-disc Sampling

Manuel N. Gamito

Lightwork Design Ltd

Steve C. Maddock

The University of Sheffield

We present an accurate and efficient method to generate samples based on a Poisson-disk distribution. This type of distribution, because of its blue noise spectral properties, is useful for image sampling. It is also useful for multi-dimensional Monte Carlo integration and as part of a procedural object placement function. Our method extends trivially from 2D to 3D or to any higher dimensional space. We demonstrate results for up to four dimensions, which are likely to be the most useful for Computer Graphics applications. The method is accurate because it generates distributions with the same statistical properties of those generated with the brute force dart-throwing algorithm, the archetype against which all other Poisson-disk sampling methods are compared. The method is efficient because it employs a spatial subdivision data structure that signals the regions of space where the insertion of new samples is allowed. The method has O(N logN) time and space complexity relative to the total number of samples. The method generates maximal distributions in which no further samples can be inserted at the completion of the algorithm. The method is only limited in the number of samples it can generate and the number of dimensions over which it can work by the available physical memory.

This paper was published in the ACM Transactions on Graphics journal. The final version of the paper is available from the ACM Digital Library. The paper was also selected for presentation at the SIGGRAPH 2010 conference. A draft version of the paper is available below:

PDF format (4.9 M) (poisson.pdf)

The source code for the prototype described in the paper is made available below.The application is written in C++ and requires the Boost library and also an implementation of the OpenGL Glut library. The application has been successfully compiled in Windows with Microsoft Visual Studio 2008 and under the Cygwin Unix emulator. The application should also compile in Linux without problems. If possible, the application should be compiled on a 64bit operating system with more than 4Gb of memory, given that the adaptive subdivision tree, used as part of the Poisson-disc sampling, can require considerable amounts of memory.

Gzipped Tar file (16 K) (poisson.tar.gz)

Some Animations from the Paper

Here are a couple of animations using the sampling method presented in the paper. They show several aspects of the sampling process in two and three dimensions. Note that the examples shown have been slowed down overall in order to visualise the sampling process better. Had these examples been presented in real time, they would have terminated too quickly for anything but the final result to be perceived. The red progress bar at the bottom of each animation indicates the percentage of space inside the unit square or cube that has been eliminated from the sampling process.

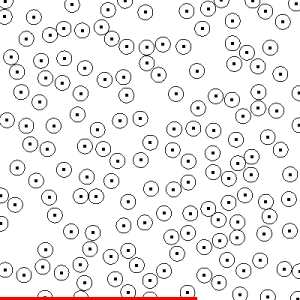	An animation that shows the generation of a 2D distribution with samples surrounded by discs of radius r/2. No discs intersect, illustrating that the distribution is correct. Quicktime MOV format (1.1M) (halfdiscs.mov)
	An animation that shows the same 2D distribution with samples surrounded by gray filled discs of radius r. No white regions are visible at the end of the clip, illustrating that the distribution is complete. Quicktime MOV format (360K) (fulldiscs.mov)
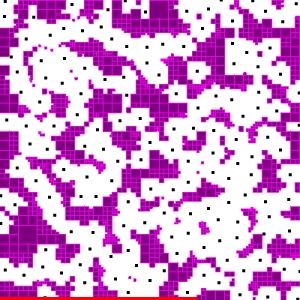	An animation that shows again the same 2D distribution and represents the leaf nodes in the subdivision tree as purple squares of several sizes. The allowable regions for insertion of new samples are contained inside the collection of leaf nodes. Quicktime MOV format (913K) (treenodes.mov)
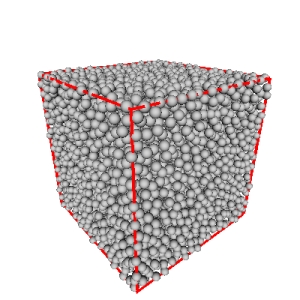	An animation that shows the generation of a 3D distribution with samples represented as spheres of radius r/2. There is no intersection between spheres. Quicktime MOV format (4.0M) (cube.mov)
	An animation that is similar to the previous one with an additional clipping plane, showing that no spheres are intersecting. Quicktime MOV format (3.6M) (cubeclipped.mov)