Autocorrelogram - A Visual Display of Sound Periodicity
Description
A C++ implementation of the autocorrelogram (ACG) model employed in (
Ma et al. 2007).
The autocorrelogram, or simply correlogram, is a visual display of sound periodicity and an important representation of auditory temporal activity that combines both spectral and temporal information. It is normally defined as a three-dimensional volumetric function, mapping a frequency channel of an auditory periphery model, temporal autocorrelation delay (or lag), and time to the amount of periodic energy in that channel at that delay and time. The periodicity of sound is well represented in the correlogram. If the original sound contains a signal that is approximately periodic, such as voiced speech, then each frequency channel excited by that signal will have a high similarity to itself delayed by the period of repetition. Primarily because it is well-suited to detecting signal periodicity, the ACG model is widely considered as the preferred computational representation of early sound processing in the auditory system.
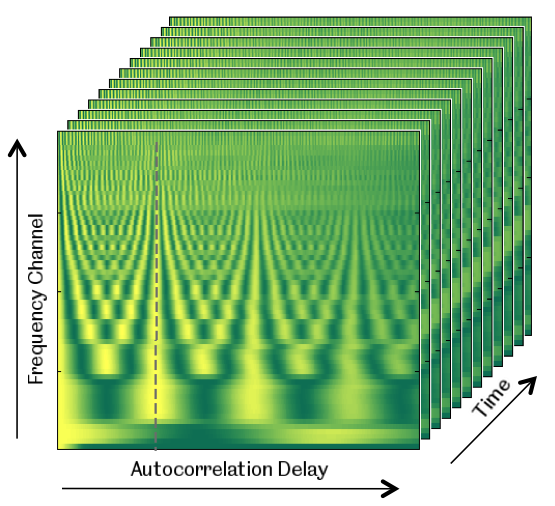
Fig. 1. Autocorrelogram for a clean speech signal spoken by a female speaker. The autocorrelogram is sampled across time and displayed as a serias of 2-dimensional graphs.
The autocorrelogram is normally sampled across time to produce a series of 2-dimensional graphs, in which frequency and autocorrelation delay are displayed on orthogonal axes (see Fig. 1). All of the frequency channels respond to a periodic signal at the rate of its fundamental frequency (F0) and this can be emphasised by summing the correlogram over all frequency channels, producing a "summary correlogram". The position of the largest peak in the summary correlogram corresponds to the F0 of the periodic sound source.
Implementation
This ACG model filters signals with a
gammatone auditory filterbank and computes a short-time autocorrelation on the output of each filter with a 30 ms Hann window. The implementation is efficient as fast Fourier transform (FFT) can be exploited to compute autocorrelations, but has an effect that longer autocorrelation delays have attenuated correlation due to the narrowing of the effective window. To compensate for this effect a normalised form of autocorrelation is used. At a given time
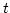
, the autocorrelation
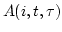
for channel
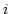
with a delay
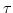
is given by
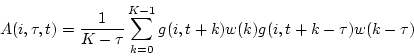
where
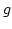
is the output of the
gammatone filterbank and
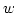
is a local Hann window of width
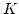
time steps. More details about this implementation can be found in (
Ma et al., 2007).
Source code
C++ source code is
available here. The program takes a WAV audio file as input and the ACG outputs are saved in a binary format as float numbers (32 bits) with a 12-byte header (3 integers) which in sequence represent the maximum delay, the number of channels and the number of frames. A Matlab script "
read_acg.m" is provided to read ACG data files of such a format. See the
README file for more details.
The
fftw3 package (http://www.fftw.org) is required to compute FFT. Compiled fftw3 libraries for Linux, Linux 64 and cygwin are included in the source code package. On a Pentium IV 2.0 GHz Linux machine the implementation runs 10 times faster than the real-time when computing 32-channel ACGs for signals sampled at 8 kHz.
Reference
- Licklider, J. (1951) A duplex theory of pitch perception. Experientia, 7:128--134.
- Slaney, M. and Lyon, R. (1990) A perceptual pitch detector. In Proc. IEEE ICASSP’90, pages 357--360, Albequerque.
- Ma, N., Green, P., Barker, J. and Coy, A. (2007) Exploiting correlogram structure for robust speech recognition with multiple speech sources. Speech Communication, 49 (12):874--891.
Acknowledgements
This autocorrelogram model was modified from a model originally suggested by Guy Brown.

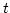 , the autocorrelation
, the autocorrelation 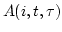 for channel
for channel 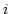 with a delay
with a delay 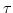 is given by
is given by
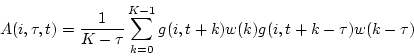
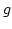 is the output of the gammatone filterbank and
is the output of the gammatone filterbank and 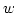 is a local Hann window of width
is a local Hann window of width 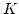 time steps. More details about this implementation can be found in (Ma et al., 2007).
time steps. More details about this implementation can be found in (Ma et al., 2007).